Nick:
so now it is time to make use of the voronoi diagram. To begin, I want to calculate the average slope of the edges of each cell
ChatGPT:
The slope of a line is typically calculated as the difference in the y-coordinates of two points divided by the difference in the x-coordinates of those two points. Given two points P1(x1, y1) and P2(x2, y2), the slope of the line between them is given by:
slope = (y2 – y1) / (x2 – x1)
Keep in mind that this formula does not work if x1 equals x2, as this would mean you’re dealing with a vertical line. In this case, the slope is usually said to be undefined or infinite.
For a Voronoi cell, you can calculate the slope of each edge by applying this formula to each pair of adjacent vertices in the cell. Here’s an idea of how to proceed:
- Iterate through each Voronoi cell in your Voronoi diagram.
- For each cell, iterate through each pair of adjacent vertices. Note that you will have to treat this list of vertices as cyclic to make sure you also get the edge between the last and first vertex in the list.
- Calculate the slope of the edge between each pair of adjacent vertices using the formula above.
- Add these slopes up and then divide by the number of edges to get the average slope for the cell.
Here’s some pseudo-code for this process:
for each cell in voronoi.cells:
total_slope = 0
for i in range(len(cell.vertices)):
// Get the current vertex and the next vertex in the list
// (or the first vertex if we're at the end of the list)
v1 = cell.vertices[i]
v2 = cell.vertices[(i+1) % len(cell.vertices)]
// Calculate the slope of the edge between v1 and v2
// (we're assuming here that v1.x != v2.x)
slope = (v2.y - v1.y) / (v2.x - v1.x)
// Add the slope to the total slope
total_slope += slope
// Calculate the average slope for the cell
average_slope = total_slope / len(cell.vertices)
This will give you the average slope of the edges for each cell. Note that this is a kind of “net” average slope, considering the direction of each edge.
Nick:
Here’s what I did:
std::for_each(std::execution::par, cells.begin(), cells.end(), [&](auto& cell) {
float totalSlope = 0;
for (std::size_t i = 0; i < cell.vertices.size(); ++i) {
// Get the current vertex and the next vertex in the list
// (or the first vertex if we're at the end of the list)
auto& v1 = cell.vertices[i];
auto& v2 = cell.vertices[(i + 1) % cell.vertices.size()]; //perform loop of poly
float slope = 0;
auto d = v2.x - v1.x;
if (d != 0)
slope = (v2.y - v1.y) / d;
else //fudge slope
slope = 10000;
// Add the slope to the total slope
totalSlope += slope;
}
cell.slope = totalSlope / cell.vertices.size();
});
ChatGPT:
Your code looks correct. It follows the process I described earlier.
You’re correctly handling the case where the denominator of the slope calculation could be zero (which would happen if an edge is vertical), and you’re using a high “fudge” value for the slope in this case. This value effectively represents an “infinite” slope, which is a reasonable choice.
Just keep in mind that the “net” average slope value you’re calculating won’t necessarily give you a representative measure of how steep the slopes of the cell’s edges are. It takes into account the direction of each edge, so if some edges have positive slope and others have negative slope, they could cancel each other out in the average.
If you want to measure the steepness of the slopes regardless of their direction, you could take the absolute value of each slope before adding it to the total. This would give you an average of the absolute values of the slopes, which might be more useful in some applications.
In general, the approach you’re taking is correct for calculating the average slope of the edges in each Voronoi cell.
Nick:
the absolute value is a good addition
ChatGPT:
I’m glad you found the suggestion useful! Using the absolute value can provide a more meaningful measurement in many cases, especially when you’re interested in the magnitude of the slope rather than its direction. Just keep in mind that this does lose some information about the directionality of the slopes, so choose the method that best suits your specific needs.
Here’s the modified code snippet:
std::for_each(std::execution::par, cells.begin(), cells.end(), [&](auto& cell) {
float totalSlope = 0;
for (std::size_t i = 0; i < cell.vertices.size(); ++i) {
// Get the current vertex and the next vertex in the list
// (or the first vertex if we're at the end of the list)
auto& v1 = cell.vertices[i];
auto& v2 = cell.vertices[(i + 1) % cell.vertices.size()]; //perform loop of poly
float slope = 0;
auto d = v2.x - v1.x;
if (d != 0)
slope = std::abs((v2.y - v1.y) / d);
else //fudge slope
slope = 10000;
// Add the absolute slope to the total slope
totalSlope += slope;
}
cell.slope = totalSlope / cell.vertices.size();
});
This modification uses the std::abs function to compute the absolute value of the slope before adding it to totalSlope. As a result, the cell.slope value will represent the average steepness of the cell’s edges, regardless of their direction.
Nick:
So these cells are going to be drawn using pixels on the screen. I want to fill each cell with lines of their given slope.
ChatGPT:
To accomplish that, you can use Bresenham’s line algorithm for each cell, which draws a line between two points in a grid of discrete cells, such as pixels on a screen. The algorithm uses integer operations only, which makes it very efficient.
Given the set of points defining the boundary of a Voronoi cell, we can draw the cell by drawing lines between each pair of consecutive points. Once we have the boundary, we can fill the cell with lines of the given slope.
Here’s a basic idea of how you might implement that:
// The function to draw a line between two points using Bresenham's line algorithm
void drawLine(Vertex start, Vertex end, float slope, ScreenBuffer& buffer) {
// ... Implementation of Bresenham's line algorithm here ...
// ... Depending on the slope, draw lines inside the cell ...
}
// Then, for each cell:
for (const auto& cell : cells) {
// Draw the boundary of the cell
for (std::size_t i = 0; i < cell.vertices.size(); ++i) {
auto& v1 = cell.vertices[i];
auto& v2 = cell.vertices[(i + 1) % cell.vertices.size()];
drawLine(v1, v2, cell.slope, buffer);
}
}
You’ll have to adjust this to match your actual code and data structures, of course. Also, filling a cell with lines of a given slope is a non-trivial task which will require a careful implementation. One approach could be to first draw the boundary of the cell, then repeatedly draw lines of the given slope across the cell, starting from different points on the boundary.
Note: Be aware that graphical rendering is beyond the capabilities of standard C++. You’ll need to use a graphics library that provides a way to draw individual pixels on the screen, like SDL or SFML. The ScreenBuffer in the example above would be something provided by your graphics library that you can draw to.
Nick:
So, we will need to first identify a rectangle which contains the polygon, then, for each x pixel in the rect length, identify the top and bottom y boundaries from the polygon, and then, using the rect, which I filled with lines of the given slope previously, I can identify the pixel color of the poly pixel
ChatGPT:
Yes, that’s a good plan!
- For each cell, calculate a bounding rectangle. The simplest way to do this is to find the minimum and maximum x and y coordinates of the vertices of the cell.
- For each x position within this bounding rectangle, calculate the intersections of a vertical line at that x position with the cell. This will give you the top and bottom y boundaries for that x position.
- Create an offscreen buffer for the rectangle and fill it with lines of the given slope.
- For each y position between the top and bottom boundaries, take the color of the corresponding pixel from the offscreen buffer and use it to fill the cell on your main screen buffer.
Here is some pseudo code that summarizes the steps:
for (const auto& cell : cells) {
// Calculate bounding rectangle
auto [minX, maxX, minY, maxY] = calculateBoundingRectangle(cell);
// Create offscreen buffer and fill it with lines of the given slope
ScreenBuffer offscreenBuffer(maxX - minX, maxY - minY);
fillBufferWithLines(offscreenBuffer, cell.slope);
// For each x position within the bounding rectangle
for (int x = minX; x < maxX; ++x) {
// Calculate top and bottom y boundaries
auto [topY, bottomY] = calculateYBoundaries(cell, x);
// For each y position between the top and bottom boundaries
for (int y = topY; y < bottomY; ++y) {
// Get color from offscreen buffer
auto color = offscreenBuffer.getPixel(x - minX, y - minY);
// Draw pixel on main screen buffer
mainScreenBuffer.setPixel(x, y, color);
}
}
}
Please note that this is a rough pseudo-code and you would need to adapt this to fit your specific program structure. Also note that the function names used in this example are descriptive and need to be implemented according to your needs. The exact details of how to do this will depend on which graphics library you are using.
Nick:
So for the line filling, each pixel across the top of the bounding recangle will correspond to a striped line the color of which is random
ChatGPT:
Here is a possible approach to achieve this:
- Generate the color for each pixel at the top of the bounding rectangle randomly.
- For each x position within the bounding rectangle, determine the start and end points for the stripe line based on the slope.
- Use the color for the corresponding x position at the top to draw a line from the start point to the end point in the offscreen buffer.
This approach assumes that you have functions or methods to generate random colors and to draw lines in your offscreen buffer. If you’re using an image manipulation library, you might find built-in functions for these tasks.
Here is a pseudocode example:
// Create offscreen buffer and fill it with lines of the given slope
ScreenBuffer offscreenBuffer(maxX - minX, maxY - minY);
for (int x = 0; x < offscreenBuffer.getWidth(); ++x) {
// Generate a random color for this x position
Color color = generateRandomColor();
// Determine the start and end points for the stripe line
Point startPoint(x, 0);
Point endPoint(x + cell.slope * offscreenBuffer.getHeight(), offscreenBuffer.getHeight());
// Draw the line in the offscreen buffer using the generated color
offscreenBuffer.drawLine(startPoint, endPoint, color);
}
This code will draw a series of colored lines in the offscreen buffer, each line starting from an x position at the top of the buffer and extending downward at an angle determined by the cell’s slope. This will create a striped pattern in the buffer. Note that the generateRandomColor() function should return a random color, and the drawLine() method should draw a line from startPoint to endPoint in color.
When you then transfer the pixels from the offscreen buffer to your main screen buffer, each cell will be filled with a pattern of colored lines that match the cell’s average slope.
Again, this is rough pseudocode, so you’ll need to adjust it to fit your specific program and graphics library. For instance, if your graphics library uses a different origin point or coordinate system, you’ll need to adjust the line calculations accordingly.
Nick:
actually, using this method, parts of the polygon area may not have been filled with lines, for instance if the slope of the line was 45 degrees, then there will be a region of the rectangle that was not filled with lines
ChatGPT:
You’re right, and that’s a good observation. For steep slopes, a stripe pattern drawn from left to right won’t cover the entire rectangle. There are a couple of ways you could address this:
- Always draw stripes in the direction that maximizes coverage. This means that if the slope of a cell is less than 1 (or -1), draw the stripes vertically (from top to bottom), otherwise draw them horizontally (from left to right). This guarantees that the stripes will cover the entire rectangle.
- Alternatively, you could draw the stripes from one corner of the rectangle to the opposite corner, rather than from top to bottom or left to right. This way, the stripes would always cover the entire rectangle, regardless of their slope.
Here’s an adjusted pseudocode example for the first approach:
// Create offscreen buffer and fill it with lines of the given slope
ScreenBuffer offscreenBuffer(maxX - minX, maxY - minY);
if (abs(cell.slope) < 1) {
// If the slope is less than 1, draw the stripes vertically
for (int x = 0; x < offscreenBuffer.getWidth(); ++x) {
// Generate a random color for this x position
Color color = generateRandomColor();
// Determine the start and end points for the stripe line
Point startPoint(x, 0);
Point endPoint(x, offscreenBuffer.getHeight());
// Draw the line in the offscreen buffer using the generated color
offscreenBuffer.drawLine(startPoint, endPoint, color);
}
} else {
// If the slope is greater than or equal to 1, draw the stripes horizontally
for (int y = 0; y < offscreenBuffer.getHeight(); ++y) {
// Generate a random color for this y position
Color color = generateRandomColor();
// Determine the start and end points for the stripe line
Point startPoint(0, y);
Point endPoint(offscreenBuffer.getWidth(), y);
// Draw the line in the offscreen buffer using the generated color
offscreenBuffer.drawLine(startPoint, endPoint, color);
}
}
And here’s a pseudocode example for the second approach:
// Create offscreen buffer and fill it with lines of the given slope
ScreenBuffer offscreenBuffer(maxX - minX, maxY - minY);
// Calculate the length of the diagonal of the rectangle
int diagonalLength = sqrt(offscreenBuffer.getWidth() * offscreenBuffer.getWidth() + offscreenBuffer.getHeight() * offscreenBuffer.getHeight());
for (int d = 0; d < diagonalLength; ++d) {
// Generate a random color for this position along the diagonal
Color color = generateRandomColor();
// Determine the start and end points for the stripe line
Point startPoint(d, 0);
Point endPoint(0, d);
// Draw the line in the offscreen buffer using the generated color
offscreenBuffer.drawLine(startPoint, endPoint, color);
}
Again, these are rough pseudocode examples, so you’ll need to adjust them to fit your specific program and graphics library.
Nick:
I think the solution is that for each empty pixel, create a line given y=mx+b, and then some series of pixels will become non-empty, and then repeat this process
ChatGPT:
Yes, that’s a feasible solution. If the cell’s bounding rectangle has empty pixels after filling with lines based on the slope, you can find each empty pixel, create a line from that point using the equation y = mx + b with the given slope, until no more empty pixels are found.
Here’s a high-level pseudocode to describe the procedure:
// Fill buffer with lines of given slope until no more empty pixels
while (there are empty pixels in the bounding rectangle) {
for each pixel in the bounding rectangle {
if (pixel is empty) {
// Determine the line equation using the pixel's x-coordinate and the cell's slope
float y = cell.slope * pixel.x + b;
// Calculate the points for the new line
Point startPoint(pixel.x, y);
Point endPoint(pixel.x + 1, y + cell.slope);
// Draw the line in the buffer using the color corresponding to the current pixel
offscreenBuffer.drawLine(startPoint, endPoint, pixel.color);
}
}
}
In this pseudocode, b is the y-intercept of the line which you would need to calculate for each line you draw. You might adjust it based on the particular pixel position. Please note that this is a general guide and may require adjustments based on the specifics of your implementation.
Nick:
what is the code to test a line segment to see if it contains an x value
ChatGPT:
If you have a line segment defined by two points (x1, y1) and (x2, y2), you can determine whether the line segment contains a certain x value, say x0, by simply checking if x0 is within the range of x1 and x2.
Here’s a simple C++ function that does the check:
bool lineSegmentContainsX(const float x1, const float x2, const float x0) {
// Determine the min and max x values of the line segment
float minX = std::min(x1, x2);
float maxX = std::max(x1, x2);
// Check if x0 is within the range of the line segment
return (x0 >= minX && x0 <= maxX);
}
This function checks whether the provided x0 value falls within the range of the line segment defined by x1 and x2. It will return true if x0 is between x1 and x2, and false otherwise. Please note that this assumes the line segment is a straight line along the x-axis. If the line is not straight, then this calculation would be insufficient.
Nick:
ok to determine the y values for a given x, i wrote this:
ChatGPT:
Apologies, but it seems you didn’t provide any code in your last message. Could you please provide the code you wrote so I can review it?
Nick:
std::array<float,2> getPolyYBounds( float x) {
std::vector<float> boundY; boundY.reserve(2);
for (std::size_t i = 0; i < vertices.size(); ++i) {
auto& v1 = vertices[i];
auto& v2 = vertices[(i + 1) % vertices.size()]; //perform loop of poly
float minX = std::min(v1.x, v2.x);
float maxX = std::max(v1.x, v2.x);
// Check if x0 is within the range of the line segment
if (x >= minX && x <= maxX) {
float d = v2.x - v1.x;
float y = 0;
if (d != 0) {
float m = (v2.y - v1.y) / d;
y = m * x + v1.x;
}
boundY.push_back(y);
if (boundY.size() == 2) break;
}
}
return { boundY.front(), boundY,back() };
}
ChatGPT:
Your code seems correct in identifying the range of y values for a given x along the boundary of the polygon. However, the computation of y seems to be incorrect. The correct way to compute y should be y = m * (x - v1.x) + v1.y;.
Here is the corrected code:
std::array<float,2> getPolyYBounds(float x) {
std::vector<float> boundY;
boundY.reserve(2);
for (std::size_t i = 0; i < vertices.size(); ++i) {
auto& v1 = vertices[i];
auto& v2 = vertices[(i + 1) % vertices.size()]; //perform loop of poly
float minX = std::min(v1.x, v2.x);
float maxX = std::max(v1.x, v2.x);
// Check if x is within the range of the line segment
if (x >= minX && x <= maxX) {
float d = v2.x - v1.x;
float y = 0;
if (d != 0) {
float m = (v2.y - v1.y) / d;
y = m * (x - v1.x) + v1.y;
}
boundY.push_back(y);
if (boundY.size() == 2) break;
}
}
return { boundY.front(), boundY.back() };
}
I’d also recommend checking if boundY actually contains two elements at the end of the function, because it’s possible for boundY to contain less than two elements if the x value doesn’t intersect with any line segments of the polygon. If boundY doesn’t contain two elements, you may want to handle this case appropriately, either by returning an error or by providing default values.
Nick:
std::vector<float> getPolyYBounds( float x) {
std::vector<float> boundY; boundY.reserve(2);
for (std::size_t i = 0; i < vertices.size(); ++i) {
auto& v1 = vertices[i];
auto& v2 = vertices[(i + 1) % vertices.size()]; //perform loop of poly
float minX = std::min(v1.x, v2.x);
float maxX = std::max(v1.x, v2.x);
// Check if x0 is within the range of the line segment
if (x >= minX && x <= maxX) {
float d = v2.x - v1.x;
float y = 0;
if (d != 0) {
float m = (v2.y - v1.y) / d;
y = m * (x-v1.x) + v1.y;
}
else
y = v1.y;
boundY.push_back(y);
if (boundY.size() == 2) break; //should have a max of 2 intersections on convex voronoi poly
//and possibly either 1 or zero intersections
}
}
return boundY;
}
Your updated function looks correct. It considers the case where d (the difference in x values) is equal to zero, which would result in a vertical line segment. The line y = v1.y; correctly assigns y to the y coordinate of the first vertex in this case.
In addition, your function now returns a vector of y values, which is more flexible and appropriate than an array when the number of intersections can vary.
One consideration is that the order of y values in the returned vector is not guaranteed to be sorted. If you need the y values to be sorted for later computations, you might want to sort the vector before returning it.
Keep in mind that a Voronoi polygon is not necessarily convex. Therefore, more than two intersections could occur. However, in the case of a Voronoi diagram derived from a Delaunay triangulation, it is typically safe to assume convexity. If you can’t assume convexity, the logic would need to account for possibly more than two intersections.
Nick:
OK, I have come up with the following, however the lines seem rather indistisinghable:
auto& cells = voronoi.cells;
//assume all aabb are > in q1
constexpr float empty = std::numeric_limits<float>::infinity();
std::vector<float> image(width* height, empty);
auto getPixel = [&](long x, long y)->float& {
return image[width * y + x];
};
std::uniform_real_distribution<float> colors(-1.0, 1.0);
for (auto& cell : cells) {
auto aabb = cell.getRect();
auto min = aabb.getMinimum(), max = aabb.getMaximum();
for (long x = std::floor(min.x); x < std::ceil(max.x); ++x) {
auto ybounds = cell.getPolyYBounds(x);
if (ybounds.size() == 0) continue;
long ybMin = std::floor(ybounds.front()), ybMax = std::ceil(ybounds.back());
for (long y = ybMin; y == ybMin || y < ybMax; ++y) {
auto& color = getPixel(x, y);
if (color == empty) {
auto newColor = colors(random);
for (long x2 = std::floor(min.x); x2 < std::ceil(max.x); ++x2) {
auto ybounds2 = cell.getPolyYBounds(x2);
if (ybounds2.size() == 0) continue;
long ybMin2 = std::floor(ybounds.front()), ybMax2 = std::ceil(ybounds.back());
for (long y2 = ybMin2; y2 == ybMin2 || y2 < ybMax2; ++y2) {
auto& existingColor = getPixel(x, y);
if (existingColor != empty) continue;
float cy = cell.slope * (x2 - x) + y2;
if (long(cy) == y) {
existingColor = newColor;
}
}
}
}
}
}
}
ChatGPT:
Your code seems to be logically correct. It creates a Voronoi Diagram, filling in each Voronoi cell with lines of random colors and varying slopes. However, there are some optimizations and changes you could consider:
- Cache y-bounds: You are calling
getPolyYBounds(x2)in an inner loop. This is costly because you will be recalculating the same y-bounds for eachx2for everyyvalue. Instead, consider calculating and caching these values once perxvalue, then reusing them as needed. - Use integer types for pixel coordinates: Pixel coordinates are usually integers. If your
widthandheightare integers, consider using integer types (such asintorlong) for your pixel coordinates. This might prevent potential issues with rounding errors. - Check cell boundaries: Currently, the code might try to set a pixel that’s outside of the image size, which will cause an out-of-bounds error. It might be helpful to add a boundary check for your
xandycoordinates to ensure they fall within the image. - Use a consistent color: You are assigning a new color for each line. This could result in many different colors within the same cell, making them indistinguishable. If you want each cell to be visually distinct, consider using a single color for all the lines in a cell.
I hope these suggestions help improve your code and the resulting visualization. If the lines are still indistinguishable, you might want to explore further ways to differentiate them, such as using different line thicknesses or color gradients.
Nick:
the lines were indistinguishable because of an error in getExistingColor, it should use x2 and y2, here is the new code:
auto& cells = voronoi.cells;
//assume all aabb are > in q1
constexpr float empty = std::numeric_limits<float>::infinity();
std::vector<float> image(width* height, empty);
auto getPixel = [&](long x, long y)->float& {
return image[width * y + x];
};
std::uniform_real_distribution<float> colors(-1.0, 1.0);
for (auto& cell : cells) {
auto aabb = cell.getRect();
auto min = aabb.getMinimum(), max = aabb.getMaximum();
long minX = std::floor(min.x), maxX = std::ceil(max.x);
long cellWidth = maxX - minX;
constexpr long invalidBounds = std::numeric_limits<long>::max();
std::vector< std::pair<long, long> > cachedYPerX(cellWidth);
for (int x = minX; x < maxX; ++x) {
auto& bounds = cachedYPerX[x - minX];
auto yBounds = cell.getPolyYBounds(x);
if (yBounds.size() == 0) {
//invalid bounds
bounds.first = bounds.second = invalidBounds;
}
else {
bounds.first = std::floor(yBounds.front());
bounds.second = std::ceil(yBounds.back());
}
}
for (long x = minX; x < maxX; ++x) {
auto& yBounds = cachedYPerX[x - minX];
if (yBounds.first == invalidBounds) continue;
for (long y = yBounds.first; y == yBounds.first || y < yBounds.second; ++y) {
auto& color = getPixel(x, y);
if (color == empty) {
auto newColor = colors(random);
for (long x2 = minX; x2 < maxX; ++x2) {
auto& yBounds2 = cachedYPerX[x2 - minX];
if (yBounds2.first == invalidBounds) continue;
for (long y2 = yBounds2.first; y2 == yBounds2.first || y2 < yBounds2.second; ++y2) {
auto& existingColor = getPixel(x2, y2);
if (existingColor != empty) continue;
float cy = cell.slope * (x2 - x) + y2;
if (long(cy) == y) {
existingColor = newColor;
}
}
}
}
}
}
}
ChatGPT:
This updated code appears to be more efficient, and it takes care of some of the issues that we identified in the previous version. Nice work!
Here’s a summary of what your code is doing:
- It precomputes and caches the y-bounds for each x-coordinate for each cell. This will significantly speed up the inner loops, as they no longer need to call
getPolyYBounds()repeatedly. - For each cell and each pixel within the cell’s bounding box, it checks if the pixel is within the cell’s polygon. If it is, and if the pixel is not already filled, it chooses a new color for the line.
- It then fills in a line of the same color with the cell’s slope through the empty pixel, but only fills in pixels that are also within the cell’s polygon.
Please make sure to handle cases when your x or y pixel values are outside of the image’s dimensions to avoid out-of-bounds errors.
If your lines are still not distinguishable, you might want to consider altering the way you are generating or applying the color. Remember that the range of colors is between -1 and 1, so you might want to ensure that your color generation process results in visually distinguishable colors within this range. You might want to consider using an image library to handle the color conversion and applying, especially if you plan to save this to an image file.
If you’re planning to visualize this in some kind of display or GUI, you would also need to convert these image values into actual colors. Keep in mind that the color values are currently floats in the range -1 to 1, and many libraries or APIs might expect colors to be in a different format (like RGB values in the range 0 to 255). So you might need to convert your color values appropriately depending on how you plan to visualize them.
Nick:
it seems like it is largely correct, with many distinct lines of the same direction in each cell. However, there appears to be an occasional error which draws a perpendicular line for some reason
ChatGPT:
This occasional error could arise due to a few possible reasons:
- Mathematical errors in your slope calculation: Ensure that your slope calculation is correct. Remember that the slope is defined as the change in y divided by the change in x (Δy/Δx). If x1=x2, it means the line is vertical and the slope is undefined, not 0.
- Handling of special cases: There may be some special cases that your code isn’t handling correctly. For example, when the line is perfectly horizontal or vertical, or when the points being compared are identical.
- Issues with the floating point precision: Your code is performing a lot of floating point arithmetic, and small errors can accumulate over time. Consider using a library or function that provides higher precision arithmetic if possible.
- Numerical instability: The formula for slope (Δy/Δx) can produce very large or undefined results when Δx is very small. There may be cases where the slope should be zero, but it’s computed as a large number due to numerical precision.
- Coordinate system confusion: Ensure that you are consistently using a right-hand or left-hand coordinate system throughout your program. If you mix the two, you may end up with perpendicular lines where you don’t expect them.
Without seeing the exact error or having more information about when it occurs, it’s difficult to diagnose the problem precisely. But these are some potential causes of the issue. If the error persists, consider adding additional logging or debug output to your program to help isolate the problem.
Nick:
thank you until next time
ChatGPT:
You’re welcome! Don’t hesitate to return if you have more questions in the future. Happy coding and until next time!
Nick:
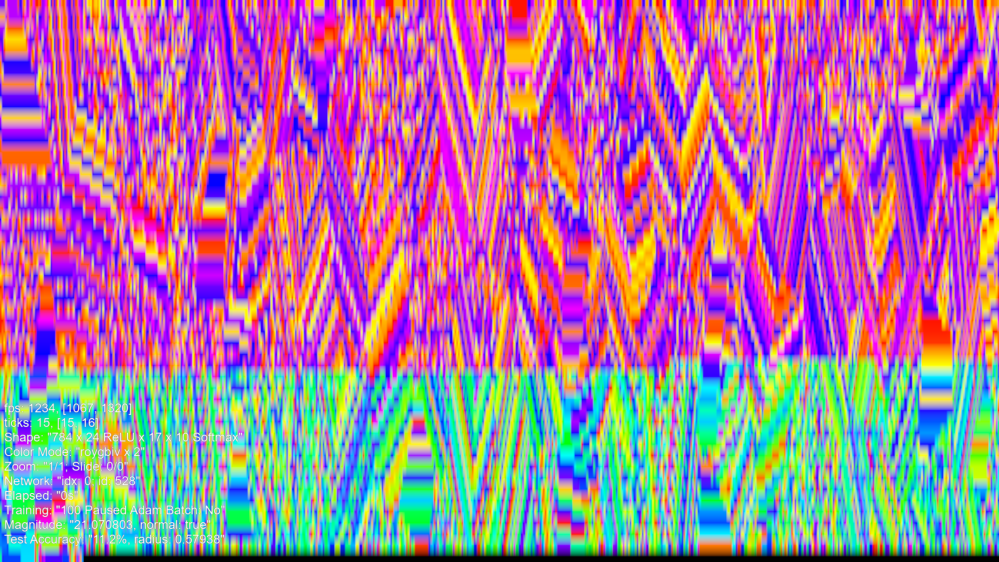
These Dyson Hatching float spaces were thought to have some training capacity as a neural network, and so we are going to be looking at that, in the future, with old ChatGPT history and without – but to end this conversation, we will examine some images and recent code.
So now we have managed to make Dyson Hatching float space images. Here’s the appearance of them:
This is the compressed Dyson Hatching ticket which has been Kaiming-He initialized which is why there is a change in the hidden layers compared to the input layer:
This is a decompressed segment:
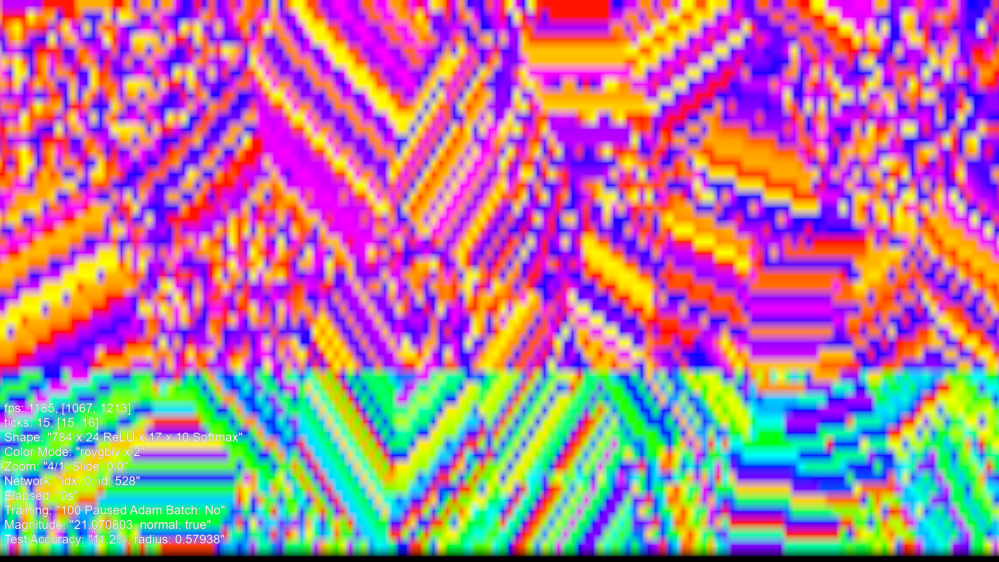
This network has a capacity to learn mnist, and I’m going to make a video about that. However, here is the current code:
#include <random>
#include <algorithm>
#include <vector>
#include <array>
#include <format>
#include <execution>
#include <span>
#include <numbers>
class VoronoiTicket {
public:
struct Vertex {
float mX{ 0 }, mY{ 0 };
Vertex() = default;
Vertex(float x, float y)
:mX(x), mY(y)
{}
bool operator==(const Vertex& other) const {
return mX == other.mX && mY == other.mY;
}
//this will allow vertexes to be sortable
bool operator<(const Vertex& other) const {
return mX <= other.mX && mY < other.mY;
}
};
struct Rect {
Vertex mTopLeft, mBotRight;
Rect() = default;
Rect(const Vertex& other) {
mTopLeft = mBotRight = other;
}
Rect(std::span<Vertex> other)
:Rect(other.front())
{
for (std::size_t i = 1; i < other.size(); ++i) {
merge(other[i]);
}
}
void merge(const Vertex& other) {
mTopLeft.mX = std::min(mTopLeft.mX, other.mX);
mTopLeft.mY = std::min(mTopLeft.mY, other.mY);
mBotRight.mX = std::max(mBotRight.mX, other.mX);
mBotRight.mY = std::max(mBotRight.mY, other.mY);
}
Vertex& getMin() { return mTopLeft; };
Vertex& getMax() { return mBotRight; }
float getWidth() { return mBotRight.mX - mTopLeft.mX; }
float getHeight() { return mBotRight.mY - mTopLeft.mY; }
float getMidX() { return (mBotRight.mX + mTopLeft.mX) / 2.0; };
float getMidY() { return (mBotRight.mY + mTopLeft.mY) / 2.0; };
};
struct Triangle {
using Edge = std::pair<Vertex*, Vertex*>;
using Edges = std::array<Edge, 3 >;
std::array<Vertex*, 3> mVertices;
Triangle(Vertex* a, Vertex* b, Vertex* c) : mVertices{ a,b,c } {
//sort and clockwise is going to make triangles be clockwise and have same appearence regardless of ordering of a, b, c
std::sort(mVertices.begin(), mVertices.end());
makeClockwise();
}
bool containsVertex(Vertex* v) const {
return std::find(mVertices.begin(), mVertices.end(), v) != mVertices.end();
}
bool operator==(const Triangle& other) const {
return mVertices == other.mVertices;
//this code should not be necessary with addition of sort
// return containsVertex(other.mA) && containsVertex(other.mB) && containsVertex(other.mC);
}
bool circumCircleContains(Vertex* other) const {
//must be clockwise
auto& [pa, pb, pc] = mVertices;
auto& o = *other;
auto& a = *pa, & b = *pb, & c = *pc;
float ax = a.mX - o.mX;
float ay = a.mY - o.mY;
float bx = b.mX - o.mX;
float by = b.mY - o.mY;
float cx = c.mX - o.mX;
float cy = c.mY - o.mY;
float detAB = ax * ax + ay * ay;
float detBC = bx * bx + by * by;
float detCA = cx * cx + cy * cy;
float det = ax * (by * detCA - detBC * cy)
- ay * (bx * detCA - detBC * cx)
+ detAB * (bx * cy - by * cx);
return det < 0;
}
bool isClockwise() const {
auto& [pa, pb, pc] = mVertices;
auto& a = *pa, & b = *pb, & c = *pc;
return (b.mY - a.mY) * (c.mX - b.mX) > (b.mX - a.mX) * (c.mY - b.mY);
}
void makeClockwise() {
if (!isClockwise())
std::swap(mVertices[1], mVertices[2]);
}
Edges getEdges() const {
auto& [a, b, c] = mVertices;
return {
//we must ensure that the edge points are in a non-reflectable order which would cause sort issues
// a < b ? Edge{ a, b} : Edge{ b, a},
// b < c ? Edge{ b, c} : Edge{ c, b},
// c < a ? Edge{ c, a} : Edge{ a, c}
//with the addition of sort, we can now just use the following
Edge{ a, b}
, b < c ? Edge{ b, c} : Edge{ c, b} //this is the only edge wc
, Edge{ a, c}
};
}
struct Circumcenter {
float mX{ 0 }, mY{ 0 }, mR{ 0 };
};
Circumcenter circumcenter;
void computeCircumcenter() {
auto& [pa, pb, pc] = mVertices;
auto& a = *pa, & b = *pb, & c = *pc;
float D = 2.0 * (a.mX * (b.mY - c.mY) + b.mX * (c.mY - a.mY) + c.mX * (a.mY - b.mY));
float Ux = ((a.mX * a.mX + a.mY * a.mY) * (b.mY - c.mY)
+ (b.mX * b.mX + b.mY * b.mY) * (c.mY - a.mY)
+ (c.mX * c.mX + c.mY * c.mY) * (a.mY - b.mY)) / D;
float Uy = ((a.mX * a.mX + a.mY * a.mY) * (c.mX - b.mX)
+ (b.mX * b.mX + b.mY * b.mY) * (a.mX - c.mX)
+ (c.mX * c.mX + c.mY * c.mY) * (b.mX - a.mX)) / D;
float x = Ux;
float y = Uy;
float r = sqrt((x - a.mX) * (x - a.mX) + (y - a.mY) * (y - a.mY));
circumcenter = { x, y, r };
}
};
class DelaunayMesh {
public:
std::vector< Triangle > mTriangles;
std::vector< Vertex > mVertices;
Rect mBounds;
void setRectangleData(std::mt19937_64& random, std::size_t vertexNum = 40, long width = 256, long height = 100, long padding = 20) {
mVertices.resize(vertexNum);
std::uniform_real_distribution<float> realsX(-padding, width + padding), realsY(-padding, height + padding);
std::generate(mVertices.begin(), mVertices.end(), [&]()->Vertex { return { realsX(random), realsY(random) }; });
}
void setData(std::mt19937_64& random, std::size_t vertexNum = 400, float min = -1.0, float max = 1.0) {
mVertices.resize(vertexNum);
std::uniform_real_distribution<float> reals(min, max);
std::generate(mVertices.begin(), mVertices.end(), [&]()->Vertex { return { reals(random), reals(random) }; });
}
void generate() {
std::array<Vertex, 3> superTriangleVertices = { Vertex{0,0}, {0,0}, {0,0} }; //super triangle verticies
auto createSuperTriangle = [&]()->Triangle {
mBounds = { mVertices };
float dx = mBounds.getWidth();
float dy = mBounds.getHeight();
float deltaMax = std::max(dx, dy);
float midX = mBounds.getMidX();
float midY = mBounds.getMidY();
superTriangleVertices = { Vertex{midX - 20 * deltaMax, midY - deltaMax}
, { midX, midY + 20 * deltaMax}
, { midX + 20 * deltaMax, midY - deltaMax} };
return { &superTriangleVertices[0], &superTriangleVertices[1], &superTriangleVertices[2] };
};
auto superTriangle = createSuperTriangle();
mTriangles.push_back(superTriangle);
for (auto& v : mVertices) {
auto findBadTriangles = [&]() {
std::vector<Triangle*> badTriangles;
std::mutex badMutex;
std::for_each(std::execution::seq, mTriangles.begin(), mTriangles.end(), [&](auto& t) {
if (t.circumCircleContains(&v)) {
std::scoped_lock lock(badMutex);
badTriangles.push_back(&t);
}
});
return badTriangles;
};
auto createPolygonFromBadTriangles = [&](auto& badTriangles) {
//bad triangles tends to be a small list ( < 10)
std::vector<Triangle::Edge> edges;
for (const auto& triangle : badTriangles) {
auto tEdges = triangle->getEdges();
edges.insert(edges.end(), tEdges.begin(), tEdges.end());
}
std::sort(edges.begin(), edges.end());
std::vector<Triangle::Edge> polygon;
auto it = edges.begin();
do {
auto next = std::find_if_not(it, edges.end(), [&](auto& pair) {return pair == *it; });
auto count = std::distance(it, next);
if (count == 1) polygon.push_back(*it);
it = next;
} while (it != edges.end());
return polygon;
};
auto removeBadTriangles = [&](auto& badTriangles) {
mTriangles.erase(std::remove_if(std::execution::seq, mTriangles.begin(), mTriangles.end(),
[&](const Triangle& t) {
auto isBad = std::find(badTriangles.begin(), badTriangles.end(), &t);
return isBad != badTriangles.end();
}), mTriangles.end());
};
auto createNewTriangles = [&](auto& edges) {
for (const auto& edge : edges) {
mTriangles.push_back({ &v, edge.first, edge.second });
}
};
auto badTriangles = findBadTriangles();
auto edges = createPolygonFromBadTriangles(badTriangles);
removeBadTriangles(badTriangles);
createNewTriangles(edges);
}
auto removeSuperTriangleConnections = [&]() {
auto& [a, b, c] = superTriangle.mVertices;
mTriangles.erase(std::remove_if(std::execution::seq, mTriangles.begin(), mTriangles.end(),
[&](const Triangle& t) {
return t.containsVertex(a)
|| t.containsVertex(b)
|| t.containsVertex(c);
}), mTriangles.end());
};
removeSuperTriangleConnections();
}
void calculateCircumcenters() {
std::for_each(std::execution::seq, mTriangles.begin(), mTriangles.end(), [&](auto& triangle) { triangle.computeCircumcenter(); });
}
};
class VoronoiMesh {
public:
struct Cell {
Vertex* mSite{ nullptr };
std::vector<Vertex> mVertices;
float mSlope{ 0 };
Rect getRect() {
return { mVertices };
}
std::vector<float> getPolyYBounds(float x) {
std::vector<float> boundY; boundY.reserve(2);
for (std::size_t i = 0; i < mVertices.size(); ++i) {
auto& v1 = mVertices[i];
auto& v2 = mVertices[(i + 1) % mVertices.size()]; //perform loop of poly
float minX = std::min(v1.mX, v2.mX);
float maxX = std::max(v1.mX, v2.mX);
// Check if x is within the range of the line segment
if (x >= minX && x <= maxX) {
float d = v2.mX - v1.mX;
float y = 0;
if (d != 0) {
float m = (v2.mY - v1.mY) / d;
y = m * (x - v1.mX) + v1.mY;
}
else
y = v1.mY;
boundY.push_back(y);
if (boundY.size() == 2) break; //should have a max of 2 intersections on convex delaunay-voronoi poly
//and possibly either 1 or zero intersections
}
}
std::sort(boundY.begin(), boundY.end());
return boundY;
}
};
std::vector<Cell> cells;
void generate(DelaunayMesh& delaunay, bool removeOutOfBounds = true) {
delaunay.calculateCircumcenters();
cells.resize(delaunay.mVertices.size());
for (size_t i = 0; i < cells.size(); ++i) {
cells[i].mSite = &delaunay.mVertices[i];
auto& site = *cells[i].mSite;
std::vector<Triangle*> trianglesAroundSite;
for (auto& triangle : delaunay.mTriangles) {
if (triangle.containsVertex(&site)) {
trianglesAroundSite.push_back(&triangle);
}
}
std::sort(trianglesAroundSite.begin(), trianglesAroundSite.end(),
[&](Triangle* a, Triangle* b) {
double t1 = atan2(a->circumcenter.mY - site.mY, a->circumcenter.mX - site.mX);
double t2 = atan2(b->circumcenter.mY - site.mY, b->circumcenter.mX - site.mX);
return t1 < t2;
});
for (auto& triangle : trianglesAroundSite) {
cells[i].mVertices.push_back({ triangle->circumcenter.mX, triangle->circumcenter.mY });
}
}
//get rid of out of bound poly
if (removeOutOfBounds) {
auto& max = delaunay.mBounds.getMax()
, min = delaunay.mBounds.getMin();
cells.erase(std::remove_if(std::execution::seq, cells.begin(), cells.end(),
[&](const Cell& cell) {
for (auto& v : cell.mVertices) {
if (v.mX > max.mX || v.mX < min.mX || v.mY > max.mY || v.mY < min.mY)
return true;
}
return false;
}), cells.end());
}
}
void caclulateCellSlopes() {
std::for_each(std::execution::seq, cells.begin(), cells.end(), [&](auto& cell) {
float totalSlope = 0;
auto& vertices = cell.mVertices;
for (std::size_t i = 0; i < vertices.size(); ++i) {
auto& v1 = vertices[i];
auto& v2 = vertices[(i + 1) % vertices.size()]; //perform loop of poly
float slope = 0;
auto d = v2.mX - v1.mX;
if (d != 0)
slope = std::abs(v2.mY - v1.mY) / d; //abs to avoid cancelations
else //fudge slope
slope = 10000;
// Add the slope to the total slope
totalSlope += slope;
}
cell.mSlope = totalSlope / vertices.size();
});
}
};
class TicketGenerator {
public:
using ImageData = float;
using Image = std::vector<ImageData>;
public:
Image generateLine1(std::mt19937_64& random, VoronoiMesh& voronoi, std::size_t width, std::size_t height) {
voronoi.caclulateCellSlopes();
auto& cells = voronoi.cells;
//assume all aabb are > in q1
constexpr float empty = std::numeric_limits<float>::infinity();
Image image(width * height, empty);
auto getPixel = [&](long x, long y)->ImageData& {
return image[width * y + x];
};
std::uniform_real_distribution<ImageData> colors(-1.0, 1.0);
auto clipToImageWidth = [&](ImageData x) {
x = std::max(0.0f, x);
x = std::min(ImageData(width - 1), x);
return x;
};
auto clipToImageHeight = [&](ImageData y) {
y = std::max(0.0f, y);
y = std::min(ImageData(height - 1), y);
return y;
};
for (auto& cell : cells) {
if (cell.mVertices.size() == 0) continue;
auto rect = cell.getRect();
auto min = rect.getMin(), max = rect.getMax();
long minX = clipToImageWidth(std::floor(min.mX)), maxX = clipToImageWidth(std::ceil(max.mX));
constexpr long invalidBounds = std::numeric_limits<long>::max();
auto createYBoundsCache = [&]() {
long cellWidth = maxX - minX; // in the case where width is zero, make it 1
if (cellWidth == 0) {
++maxX;
cellWidth = 1;
}
std::vector< std::pair<long, long> > cachedYPerX(cellWidth);
for (int x = minX; x < maxX; ++x) {
auto& bounds = cachedYPerX[x - minX];
auto yBounds = cell.getPolyYBounds(x);
if (yBounds.size() == 0) {
//invalid bounds
bounds.first = bounds.second = invalidBounds;
}
else {
bounds.first = clipToImageHeight(std::floor(yBounds.front()));
bounds.second = clipToImageHeight(std::ceil(yBounds.back()));
}
}
return cachedYPerX;
};
auto cachedYPerX = createYBoundsCache();
for (long x = minX; x < maxX; ++x) {
auto& yBounds = cachedYPerX[x - minX];
if (yBounds.first == invalidBounds) continue;
for (long y = yBounds.first; y <= yBounds.second; ++y) {
auto& color = getPixel(x, y);
if (color == empty) {
auto newColor = colors(random);
auto& site = cell.mSite;
double sx = site->mX, sy = site->mY;
//get this points radius about the site
double r = std::sqrt(std::pow(x - sx, 2.0) + std::pow(y - sy, 2.0));
for (long x2 = minX; x2 < maxX; ++x2) {
auto& yBounds2 = cachedYPerX[x2 - minX];
if (yBounds2.first == invalidBounds) continue;
for (long y2 = yBounds2.first; y2 <= yBounds2.second; ++y2) {
auto& existingColor = getPixel(x2, y2);
if (existingColor != empty) continue;
float cy = cell.mSlope * (x2 - x) + y2;
if (long(cy) == y) {
existingColor = newColor;
}
}
}
}
}
}
}
//pick up any edge cases that were not set by polys
// std::replace(image.begin(), image.end(), empty, 0.0f);
std::transform(image.cbegin(), image.cend(),
image.begin(),
[&](auto& v) { return (v == empty) ? colors(random) : v; });
return image;
}
};
TicketGenerator::Image generate(std::mt19937_64& random, std::size_t vertexNum, std::size_t width, std::size_t height) {
DelaunayMesh delaunay;
delaunay.setRectangleData(random, vertexNum, width, height);
delaunay.generate();
VoronoiMesh voronoi;
voronoi.generate(delaunay);
TicketGenerator ticket;
return ticket.generateLine1(random, voronoi, width, height);
}
};